盲目搜索

• 按照预先设定好的搜索策略进行搜索，并且不根据搜索过程中获得的中间信息更改控制策略。又称无信息搜索，需要大量的时间和空间作为基础

深度优先搜索Depth First Search（DFS）

• 过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次 -
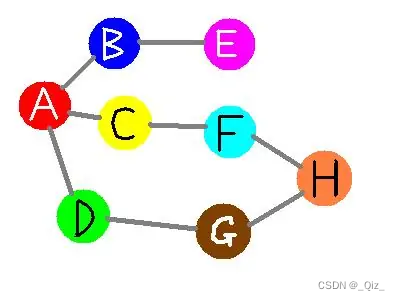
• 搜索顺序为A-B-E-C-F-H-G-D

宽度优先搜索Breadth First Search（BFS）

• 过程简要来说是按照深度搜索每一个可能的分支路径，而且每个节点只能访问一次 -
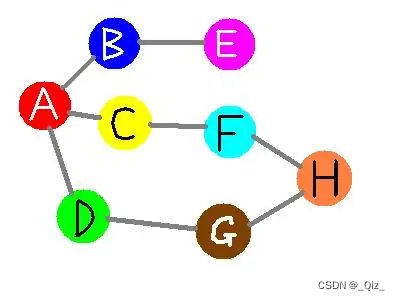
• 搜索顺序为A-B-C-D-E-F-G-H
• 从起点开始，首先遍历起点周围邻近的点，然后再遍历已经遍历过的点邻近的点，逐步的向外扩散，直到找到终点。
• 
• 相邻之间节点的移动代价相同

Dijkstra算法

• 考虑这样一种场景，在一些情况下，图形中相邻节点之间的移动代价并不相等。例如，游戏中的一幅图，既有平地也有山脉，那么游戏中的角色在平地和山脉中移动的速度通常是不相等的。

• 由荷兰计算机科学家Edsger W. Dijkstra在1956年提出的。

• Dijkstra适合计算权值不为负的有向图的最短路径长度。Dijkstra也称作单源路径算法，给定图中的一个起点start point,算法可以计算出从起点到图中任意一个节点的最短距离。

• 在Dijkstra算法中，需要计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序。

• 每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。

• 由于贪心的选择了代价最小的点，每次该点第一次被访问到，该代价就是起点到该点的代价

• 举例示意：

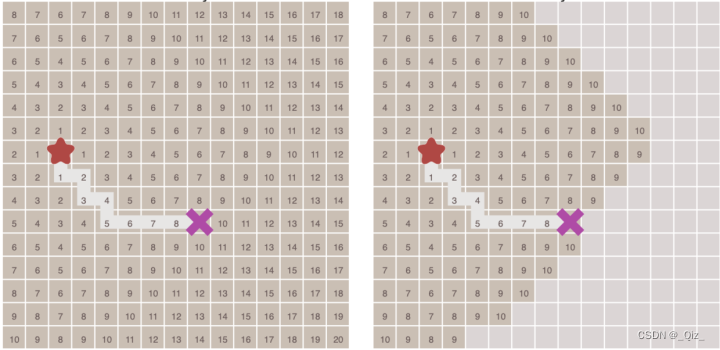
• 对比了不考虑节点移动代价差异的广度优先搜索与考虑移动代价的Dijkstra算法的运算结果
  

• 堆优化Dijkstra代码示意：

启发式算法

• 启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离距离一般不能被预计。（根据搜索过程中获得的中间信息更改控制策略，通过启发函数引导算法的搜索方向）
• 蚁群算法、模拟退火、神经网络、梯度下降、A*、爬山法等

最简单启发式算法之一的A*算法为例

概述

• 最初发表于1968年，由Stanford研究院的Peter Hart, Nils Nilsson以及Bertram Raphael发表。它可以被认为是Dijkstra算法的扩展。

• A* 算法，A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。

• 核心部分：估值函数：

• 

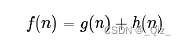
  • f(n)表示当前估价函数
  • g(n)为当前真实代价，n为搜索终点即为最终求解结果
  • h(n)为当前节点到目标节点的估计值
    • 估价值h(n)<= n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低，但能得到最优解。
    • 如果 估价值>实际值,搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。
    • 估价值与实际值越接近，估价函数取得就越好。
  • A*算法使用两个集合来表示待遍历的节点，与已经遍历过的节点，这通常称之为open_set和close_set

算法实现以及应用举例

• 算法描述：

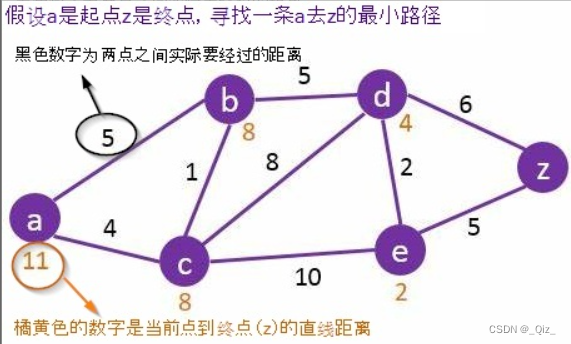
• 算法实现

  • 通过扩展Dijkstra 实现，以堆优化Dijkstra算法为例，每次入堆时同时存储f(n)、g(n)、h(n)三个信息，利用贪心的思想通过推每次选取最小的f(n)，最终找到目标。

• A*代码示意：

• 应用举例
  • 求n个点的有向图中，起点s到终点t的第k短路，路径允许重复经过点或者边
  • 要求出最优解，h(n)估值必须小于等于实际值，由于是求第k短路，可以选取终点到各个点的最短路距离为估计值

• 加入估价函数后搜索与BFS搜索对比
  
• A*算法与广度、深度优先和Dijkstra 算法的联系就在于：当g(n)=0时，该算法类似于DFS，当h(n)=0时，该算法类似于BFS。且同时，如果h(n)为0，只需求出g(n)，即求出起点到任意顶点n的最短路径，则转化为单源最短路径问题，即Dijkstra算法。

估价函数举例（以距离为例）

• 曼哈顿距离
  如果在一个图形中只允许上下左右四个方向移动，则启发函数可以使用曼哈顿距离
  
• 对角距离
  如果图形中允许斜着朝邻近的节点移动，则启发函数可以使用对角距离。
  
• 欧几里得距离
  如果图形中允许朝任意方向移动，则可以使用欧几里得距离。
• 需要根据具体情况，选择不同估价函数（最短距离、编辑距离等等）
  

定义

有很多问题并没有最优的解，或是要计算出最优的解要花费很大的计算量，面对这类问题一般的做法是利用迭代的思想尽可能的逼近问题的最优解。我们把解决此类优化问题的方法叫做优化算法，优化算法本质上是一种数学方法，是高维函数优化问题的解决方法。
（个人理解：还是一种搜索算法）

现代优化算法

现代优化算法是20世纪80年代初以来得到深入研究和广泛应用的启发式算法。主要包括贪婪算法(greedy algorithm)模拟退火算法，遗传算法，蚁群优化算法，人工神经网络算法，梯度下降算法等。

优点

相比于最优化算法，启发式算法能够迅速发展的优点：

• 数学模型本身是实际问题的简化，或多或少地忽略了一些因素；而且数据采集具有不精确性；参数估计具有不准确性；这些因素可能造成最优算法所得到的解比启发式算法所得到的解更差。
• 有些难的组合最优化问题可能还没有找到最优算法（例如NP-Hard问题），即使存在，由算法复杂性理论，它们的计算时间是无法接受或不实际的。
• 一些启发式算法可以用在最优算法中。如在分枝定界算法中，可以用启发式算法估计下（上）界。

高维函数优化问题

概述

• 指具有两个以上变量的函数
• 函数维度增加后造成的问题：
  • 各维度分量之间排列组合关系使得高维函数所需要搜索的定义域空间非常复杂
  • 搜索空间规模随着维度的增加呈现指数级增长
• 盲目搜索虽然能保证找到最优解，但所需算力太大，搜索时间太长，难以找到答案
• 目前基本使用启发式思想设计优化算法

应用

几乎所有的机器学习算法最后都归结为求一个目标函数的极值，即最优化问题。

对于有监督学习

我们要找到一个最佳的映射函数f(x)，使得对训练样本的损失函数最小化（最小化经验风险或结构风险）：
$$\underset{\mathrm{w}}{\min }\frac{1}{N}\sum _{i=1}^{N}L\left(\mathrm{w},{\mathrm{x}}_i,{\mathrm{y}}_i\right)+\lambda \Vert \mathrm{w}{\Vert }_2^2$$
N为训练样本数，L是对单个样本的损失函数，w是要求解的模型参数，是映射函数的参数，xi为样本的特征向量，yi 为样本的标签值。
或是找到一个最优的概率密度函数ρ(x)，使得对训练样本的对数似然函数极大化（最大似然估计）：
$$\max \sum _{i=1}^l\ln p\left({\mathrm{x}}_i;\theta \right)$$
在这里，θ是要求解的模型参数，是概率密度函数的参数。

对于无监督学习

以聚类算法为例，算法要是的每个类的样本离类中心的距离之和最小化：
$$\underset{\mathrm{S}}{\min }\sum _{i=1}^k\sum _{\mathrm{x}\in S_i}{\Vert \mathrm{x}?{\mu }_i\Vert }^2$$
在这里k为类型数，x为样本向量，ui为类中心向量，Si为第i个类的样本集合。

• 总体来看，机器学习的核心目标是1.给出一个模型（一般是映射函数），2.定义对这个模型好坏的评价函数（目标函数），3.求解目标函数的极大值或者极小值，以确定模型的参数，从而得到我们想要的模型。在这三个关键步骤中，前两个是机器学习要研究的问题，建立数学模型。第三个问题是纯数学问题，即高维函数优化方法。

举例：梯度下降

梯度的方向告诉我们哪个方向上升的最快，它的幅值则表示最陡峭的上升/下降有多陡。所以，在最小值的地方，曲面轮廓几乎是平坦的，我们期望得到几乎为零的梯度。事实上，最小值点的梯度就是 0

参数更新基本方程：
$$\omega \leftarrow \omega ?\alpha ?{?}_w\sum _1^m{L}_m(w)$$
对所有的权重同时更新，不断重复，直到收敛。

梯度下降的挑战和问题

学习率较大，可能会达到最小值点，也有可能迈过了最小值点
学习率较小，可能会滞留在极小值点附近。

1元函数举例

$$y=x^2+1,y^{\prime }=2x$$

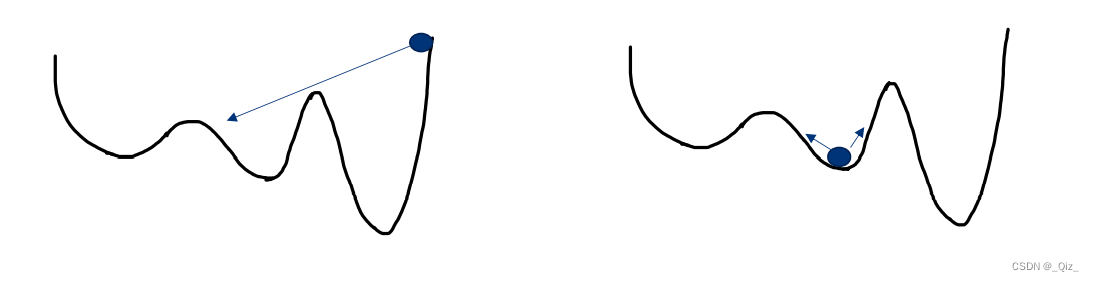
挑战1：局部极小值

在实际求解的过程中，求解函数图像往往是这样的：

A附近为极小值点，算法很可能直接收敛到该极小值点，而无法到达最小值点

挑战2：鞍点

一旦到达梯度为 0 的区域，不管极小值点的质量如何，它都几乎无法逃离。我们面临的另一种问题是鞍点，它们的形状如下：

之前的图片中看到两座山峰相遇时候的鞍点。

鞍点得名于它的形状类似于马鞍。也是梯度为0的点，尽管它在 x 方向上是一个最小值点，但是它在另一个方向上是局部最大值点，并且，如果它沿着 x 方向变得更平坦的话，梯度下降会在 x 轴振荡并且不能继续根据 y 轴下降，这就会给我们一种已经收敛到最小值点的错觉。

解决方法

使用可变的学习率
梯度下降中常用的一个技术是采用可变的学习率，而不是固定的学习率。初始时，我们可以使用较大的学习率。但是到了后来，随着接近最小值点，我们需要慢下来。

随机梯度下降

每次更新时用一个样本，所谓随机就是用样本中的一个例子来近似我所有的样本

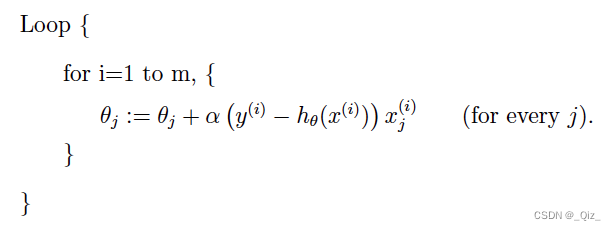
速度快，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

小批量（mini-batch）梯度下降
解决只选取一个样本结果可能不够准确的问题，是一种折中的办法
每次更新时采用b个样本，这些小样本的梯度来近似所有样本梯度

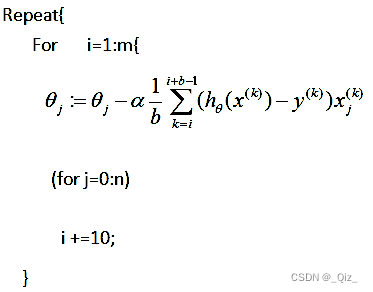
优化算法存在的问题：对不同的优化函数以及不同的维数需要不断改变算法的实验参数，以此获得较好的收敛结果